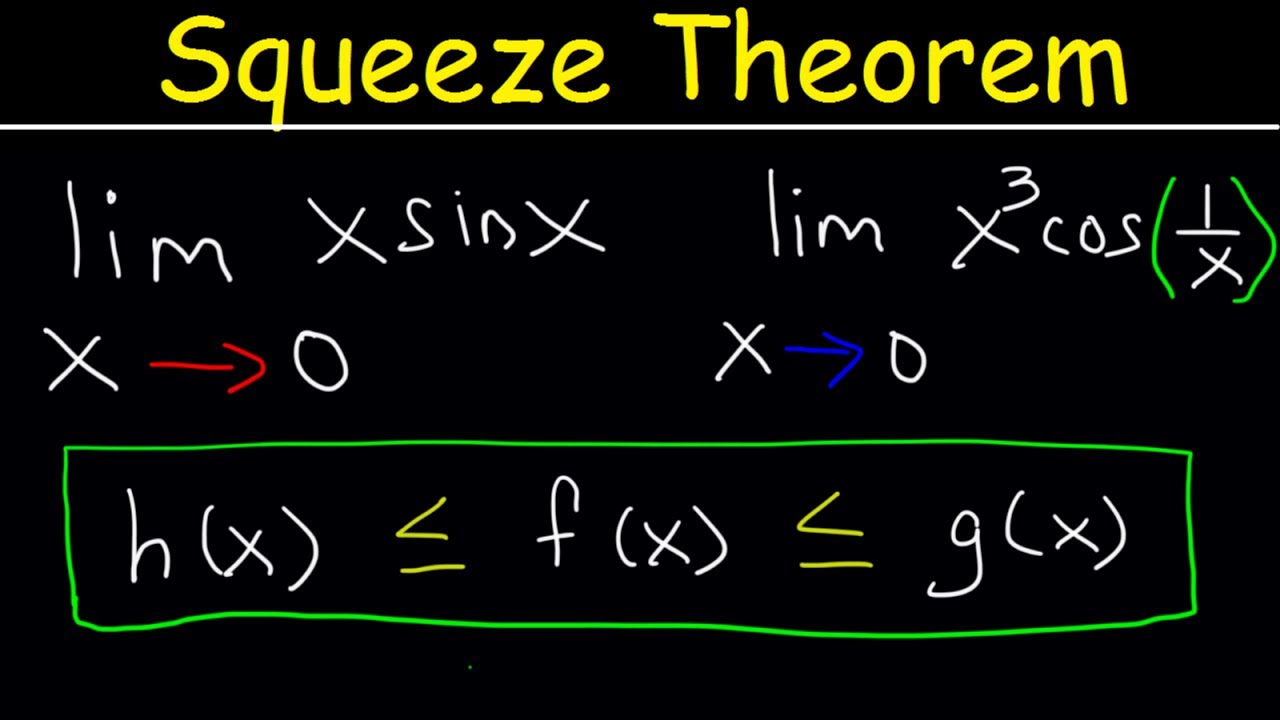The Art Of Limiting: Understanding The Squeeze Theorem
The Squeeze Theorem is a fundamental concept in calculus that serves as a powerful tool for determining the limits of functions. It plays a crucial role in evaluating limits that might seem elusive at first glance. This theorem is particularly useful in cases where direct substitution fails or when the function exhibits ambiguous behavior as it approaches a certain point. By establishing bounds for a function, we can effectively "squeeze" it into a limit, allowing us to ascertain its behavior in a manner that is both intuitive and mathematically rigorous.
At its core, the Squeeze Theorem states that if we have three functions, f(x), g(x), and h(x), where f(x) ≤ g(x) ≤ h(x) in a neighborhood around a point, and if the limits of f(x) and h(x) as x approaches that point are equal, then the limit of g(x) must also equal that same value. This theorem not only simplifies the process of finding limits but also enhances our understanding of continuity and the behavior of functions near specific points.
In this article, we will delve deeper into the Squeeze Theorem, exploring its applications, providing illustrative examples, and answering some commonly asked questions. Whether you're a student grappling with calculus concepts or simply interested in the mechanics of limits, the Squeeze Theorem is an essential topic that can illuminate the intricacies of mathematical analysis.
What Is the Squeeze Theorem?
The Squeeze Theorem is often described in terms of inequalities. To be more specific, if we have three functions: f(x), g(x), and h(x), the theorem asserts that if:
- f(x) ≤ g(x) ≤ h(x) for all x in some interval around a point c (except possibly at c itself),
- lim x→c f(x) = L,
- lim x→c h(x) = L,
Then:
lim x→c g(x) = L.
How Does the Squeeze Theorem Work?
The Squeeze Theorem operates on the principle of bounding a function between two other functions. By demonstrating that two simpler functions converge to the same limit, we can assert that the more complex function must also converge to that limit. This is particularly useful in cases where direct evaluation of the limit is challenging or impossible without additional manipulation.
What Are Some Examples of the Squeeze Theorem?
To illustrate the Squeeze Theorem, consider the following example involving the function g(x) = x² sin(1/x) as x approaches 0. Direct substitution leads to an indeterminate form, but we can use the Squeeze Theorem to resolve this:
- We know that -1 ≤ sin(1/x) ≤ 1 for all x ≠ 0.
- Multiplying through by x² (which is non-negative) gives us:
- -x² ≤ x² sin(1/x) ≤ x².
Now, we can evaluate the limits of the bounding functions:
- lim x→0 -x² = 0
- lim x→0 x² = 0
Since both bounding functions converge to 0, by the Squeeze Theorem, we conclude:
lim x→0 x² sin(1/x) = 0.
When Is the Squeeze Theorem Applicable?
The Squeeze Theorem is particularly applicable in the following scenarios:
- When evaluating limits that exhibit oscillatory behavior.
- In cases where direct substitution results in indeterminate forms (like 0/0 or ∞/∞).
- When the function is bounded by two simpler functions whose limits are known.
Why Is the Squeeze Theorem Important in Calculus?
The importance of the Squeeze Theorem in calculus cannot be overstated. It provides a systematic method for finding limits that might otherwise be challenging to evaluate. Moreover, it fosters a deeper understanding of the behavior of functions, particularly in the context of continuity and differentiability. The theorem also opens the door to more advanced topics in analysis, such as the study of sequences and series.
How to Use the Squeeze Theorem Effectively?
To effectively use the Squeeze Theorem, follow these steps:
- Identify the function g(x) whose limit you want to evaluate.
- Find two functions f(x) and h(x) such that f(x) ≤ g(x) ≤ h(x) in the vicinity of the point of interest.
- Verify that the limits of f(x) and h(x) are equal as x approaches the specified point.
- Conclude that lim x→c g(x) must equal that same limit.
Can the Squeeze Theorem Be Used in Real-World Problems?
Yes, the Squeeze Theorem can be applied to various real-world problems, particularly in fields such as physics, engineering, and economics. For instance:
- In physics, the Squeeze Theorem can help analyze the behavior of oscillating systems, such as a pendulum or a spring.
- In engineering, it can be used to assess the limits of certain materials under stress.
- In economics, the theorem may assist in determining the limits of profit or cost functions in specific scenarios.
Conclusion: The Squeeze Theorem in a Nutshell
The Squeeze Theorem is a valuable concept in calculus that enables mathematicians and students alike to evaluate limits with greater ease and confidence. By bounding a function between two others, we can determine its limit without direct evaluation. This theorem not only simplifies complex problems but also enhances our understanding of functions and their behaviors. Whether you're studying calculus or applying these concepts to real-world scenarios, the Squeeze Theorem is an indispensable tool in your mathematical toolkit.
Exploring The World Of Passport Bros: Adventures Beyond Borders
Unlocking The Secrets Of SextPanther: The Ultimate Adult Messaging Platform
Unraveling The Mystery Of Jdfromny Twitter: A Unique Perspective